The particular QKD scheme that we will describe was proposed by Charles Bennett and Gilles Brassard in 1984, and is often referred to as BB84.
The protocol has two main parts, a quantum and classical phase. In the quantum phase, Alice sends single photons to Bob over some public quantum channel. In the classical phase, Alice and Bob need to talk to each other over an authenticated classical channel, that is, it can be public but they need to verify that they are talking to the correct person.
Recall that light is an EM wave, that is a wave of paired electric fields and magnetic fields that are perpendicular to each other. If the electric field component of a beam of light vibrates along a single direction (like vertical in the figure below), we say that the beam of light is polarized in that direction.
The polarization can be measured using polarizing filters, which is made of a special material that blocks one of two perpendicular directions.
For BB84, it is enough to consider two kinds of polarizing filters. The first one we shall call the $+$ filter, since it involves the horizontal and vertical directions. The other one we shall call the $\times$ filter, since it involves the left-diagonal (\) and right-diagonal (/) directions.
 |
| Alice and Bob agree on a bit table for encoding 0 and 1 in both the $+$ filter and $\times$ filter. |
To perform BB84, Alice and Bob have to first agree on how bits will be encoded in the polarization directions for each filter. This means they should form a bit table like the one shown above.
Once they have setup the table, the scheme begins with Alice producing a random string of bits and a random sequence of filters. She then prepares photons which are polarized in the directions according to the agreed-upon bit table, as illustrated below. She sends the photons one by one to Bob.
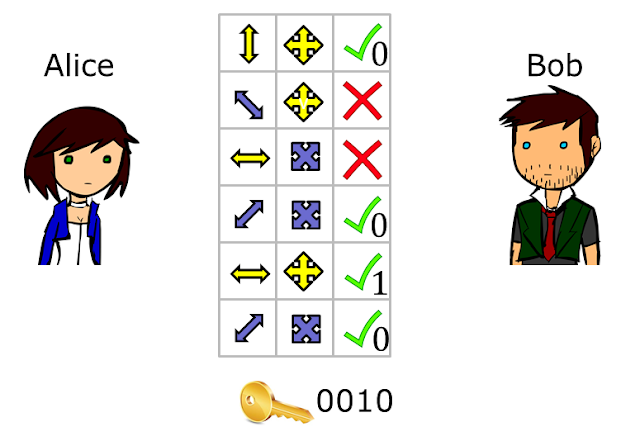
On his end, Bob created his own random sequence of filters that he will use to measure the photons he gets from Alice (figure below). He translates the outcome of each measurement into bits using the bit table. Observe here that if Bob measures the polarized photon using a filter that does not match the filter chosen by Alice, then he gets a random outcome, that is, both 0 and 1 are equally likely for that filter. In quantum terms, this is because each polarization of the $+$ filter can be thought of as an equal superposition of polarization directions of the $\times$ filter, and vice-versa.
At this point, the quantum phase of the scheme is done. For the classical phase, Alice and Bob can talk over the phone to perform the remaining step. Here Alice tells Bob what filters she used for sending each photon (but not the direction) and Bob tells Alice in which positions they used the same filter. The bits produced from the positions with matching filters will be identical and the resulting bit string is called the raw key.
It is important to note that it is okay for Alice and Bob to reveal the filters because even if an eavesdropper named Eve listened in, knowing just the filters after the quantum phase gives no information about the bits.
 |
| Alice and Bob compare the filters they used over some authenticated classical channel. The positions where the filters match correspond to identical bits, so these together form their raw key. |
Of course, you might think that Eve would try something clever, like copy the photon polarization into some quantum memory so she can measure it later when the filters are revealed. However, we know from quantum theory that you can not copy arbitrary quantum states so the only way this copying tactic will work is if she already knew what polarization she was trying to copy.
But what if Eve instead uses her own filter to measure photons and prepares new photons for Bob based on the outcome of her measurements? This sounds fine except that when Eve measures with the wrong filter and Bob measures with the right one,there is a 50-50 chance that Alice and Bob record different bits even though they used the same filter. Alice and Bob can actually use some of the raw key bits to detect such a discrepancy, especially if Eve tried to measure too many of the photons.
In a more realistic setting, when Alice sends a polarized photon to Bob, the photon Bob gets might already have a different polarization direction. This would lead to a few cases where the bits don't match for Alice and Bob even though they use the same filter.
In this case, Alice and Bob have to perform additional steps to correct for errors. This requires sacrificing some of the bits of the raw key for testing and correcting. Note that error correction corrects errors regardless of its source, so this also corrects for errors that are caused by Eve.
This testing itself will reveal some information to Eve about the raw key, which might be useful to her. Therefore, Alice and Bob have to do privacy amplification next to reduce whatever useful information Eve might have gained from the error correction step. The bit string that they obtain after error correction and privacy amplification is the final secret key.
When we say that the key is secret, what we really mean is that if Eve that was trying to figure out the key, Alice and Bob can always detect Eve's presence by using some of the bits in the raw key for checking the error rate. When the error rate is above an acceptable level, Alice and Bob conclude that somebody has been eavesdropping and they discard the raw key.
References:
Charles Bennett and Gilles Brassard, Quantum cryptography: Public key distribution and coin tossing in Proc. IEEE ICCSSP vol. 1 (1984) 175-179.



No comments:
Post a Comment