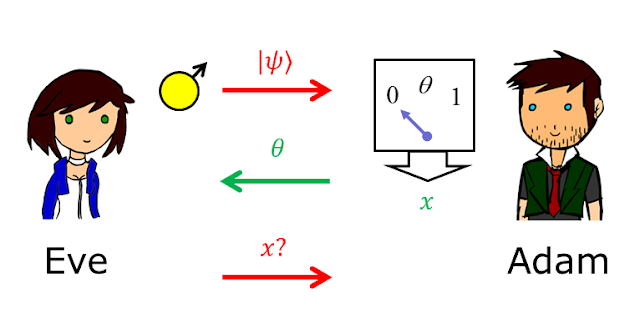
We will consider a guessing game that shows security against an eavesdropper Eve who can prepare quantum states but otherwise store and process classical information only. For example, Eve is allowed to make measurements on a qubit during its transmission but she does not possess any quantum memory for storing quantum states that she might entangle with the qubit.
In such a setting, Eve's actions effectively chooses the state of the qubit sent to Adam, since she would know as much as she can about the qubit if she had prepared it herself. This situation can be analyzed in terms of the following guessing game, to be played by Adam and Eve:
1. Eve prepares a qubit $| \psi \rangle$ and sends it to Adam.
2. Adam chooses a uniformly random bit $\theta$. If $\theta = 0$, Adam measures $| \psi \rangle$ in the standard basis $\{ |0\rangle, |1\rangle \}$. If $\theta = 1$, Adam measures $| \psi \rangle$ in the Hadamard basis $\{ |+\rangle, |-\rangle \}$, where $|\pm\rangle = (|0\rangle \pm |1\rangle )/ \sqrt{2}$.
3. Adam records a bit value $x$ as his measurement outcome. (By convention, $|+\rangle$ corresponds to bit value 0.)
4. Adam reveals the measurement basis $\theta$ to Eve.
Eve wins the game if she correctly guesses the value of $x$.
 |
| The uncertainty guessing game, Eve prepares a qubit in state $|\psi \rangle$ and sends it to Adam. Adama randonly chooses a bit $\theta$, which he uses to decide whther to measure the qubit in the standard basis $\theta = 0$ or the Hadamard basis $\theta = 1$. In either case, Adam obtains a bit value $x$. Eve's goal is to guess Adam's result. |
This game embodies the uncertainty principle because for incompatible measurements such as the standard and Hadamard basis, there is no quantum state that Eve can prepare that allows her to perfectly guess the outcome for both choices of measurements. In this case, uncertainty can be quantified in terms of Eve's average winning probability:
$ \Pr [\text{Eve wins}] = ( \Pr [ x \text{ is guessed correctly} | \theta = 0] + \Pr[ x \text{ is guessed correctly} | \theta = 0] )/2 \le c $.
The above inequality holds since the basis is chosen uniformly at random. Now we will show that if Eve has no additional information except for the basis announced by Adam, then the bound $c$ is strictly less than 1.
We want to find the largest possible $c$ that Eve can achieve. To do this, Eve needs to find a state $ | \psi \rangle$ that maximizes her guessing probability in both bases because she does not know which basis Adam will measure.
Intuitively she has to prepare a state where she know one of the outcomes is significantly more likely for both bases, so she can make that her guess. It should not matter which outcome is more likely, only that Eve knows which one it is for a given basis $\theta$. So we do not lose generality if we look for the state such that $x = 0$ is more likely for either basis.
We also know that there is no observable physical difference between $| \psi \rangle$ and $e^{i \phi} | \psi \rangle$, which lets us consider
$|\psi \rangle = a | 0 \rangle + (b+ i c) | 1 \rangle $ with $ a^2 + b^2 + c^2 = 1$.
Now we have
$\Pr[x = 0 | \theta = 0] = | \langle 0 | \psi \rangle |^2 = a^2 $, and
$\Pr[x = 0 | \theta = 1] = | \langle + | \psi \rangle |^2 = \left| \dfrac{(a + b + ic) }{\sqrt{2}} \right|^2 = \dfrac{(a + b)^2 + c^2}{2}$.
Since each $\theta$ is equally likely,
$\Pr[x = 0 ] = \dfrac{a^2}{2} + \dfrac{(a + b)^2 + c^2}{4}$.
Let $f(a,b,c) = \Pr[x = 0]$. We want to maximize $f(a,b,c)$ subject to the constraint $g(a,b,c) = a^2 + b^2 + c^2 - 1 = 0$. There are several ways to do this; here we will present two.
The conventional approach here is to use the method of Lagrange multipliers. For this method, we define $ \mathcal{L} = f(a,b,c) + \lambda g(a,b,c)$, where $\lambda$ is a Lagrange multiplier.
We take partial derivatives and set them to zero, and we would get candidate solutions for minimum and maximum values:
$
\begin{align}
\nonumber
\dfrac{\partial \mathcal{L}}{\partial \lambda} &= a^2 + b^2 + c^2 - 1 = 0,
&
\dfrac{\partial \mathcal{L}}{\partial a} &= a + \dfrac{a+b}{2} + 2 \lambda a = 0, \\
\nonumber
\\
\nonumber
\dfrac{\partial \mathcal{L}}{\partial b} &= \dfrac{a+b}{2} + 2 \lambda b = 0,
&
\dfrac{\partial \mathcal{L}}{\partial c} &= \dfrac{c}{2} + 2 \lambda c = 0.
\end{align}
$
The first equation is just the constraint. From the last equation, either $\lambda = -1/4 $ or $c = 0$. If we take the first one and plug into the third equation, we get
$ \dfrac{a+b}{2} - \dfrac{b}{2} = 0 \quad \implies \quad a = 0 $,
which if we substitute into the second equation gives $b = 0$. Finally, the first equation implies $c = \pm 1$ and thus $|\psi\rangle = \pm i |1\rangle$. So this solution actually minimizes the outcome $x = 0$ since for this state $ \Pr[x = 0 | \theta = 0] = 0$ and $ \Pr[x = 0 | \theta = 1] = 1/2$.
We get the maximum from taking $c = 0$, which means $a^2 + b^2 = 1$, and from the second and third equations:
$ -2 \lambda = 1 + \dfrac{a+b}{2a} = \dfrac{a+b}{2b}$.
It follows from the middle and right-hand-sides above that $a^2 - b^2 = 2 a b$. Using the constraint with $c = 0$ here leads to
$a^2 - b^2 = a^2 - ( 1 - a^2) = 2 a b = 2 a \sqrt{1 - a^2}$.
Squaring both sides gives
$(2 a^2 -1)^2 = 4 a^2 ( 1- a^2) \quad \implies \quad 8 a^4 - 8 a^2 + 1 = 0$.
Therefore by the quadratic formula, we obtain
$a^2 = \dfrac{8 \pm \sqrt{64 - 4(8)}}{2(8)} = \dfrac{2 + \sqrt{2}}{8}$.
The larger value has a plus sign so
$a = \sqrt{\dfrac{2 + \sqrt{2}}{8}} = \sqrt{\dfrac{1}{2} \left( 1 + \dfrac{1}{\sqrt{2}} \right)} = \cos \left(\frac{\pi}{8}\right)$, and so $b = \sin\left(\frac{\pi}{8}\right)$.
$\Pr[x = 0] = \dfrac{1}{2}\cos^2 \left( \frac{\pi}{8}\right) + \dfrac{1}{4} + \dfrac{1}{2} \cos\left(\frac{\pi}{8}\right) \sin\left( \frac{\pi}{8}\right) = \dfrac{1}{2}\cos^2 \left( \frac{\pi}{8}\right) + \dfrac{1}{4} [1 + \sin\left( \frac{\pi}{4} \right) ] $
$ \qquad \qquad = \dfrac{1}{2} \left( 1 + \dfrac{1}{\sqrt{2}} \right) = \cos^2 \left(\frac{\pi}{8}\right)$.
A different way get to the result is to note that if we define
$M = \dfrac{1}{2} \left( | 0 \rangle \langle 0 | + | + \rangle \langle + |\right) $
then $\Pr[x = 0] = \langle \psi | M | \psi \rangle$. We can maximize this by looking for an eigenstate $|m\rangle$ of M, which corresponds to its maximum eigenvalue $\omega$. In that case,
$\Pr[x = 0] = \langle m | M | m \rangle = \langle m | \omega | m \rangle = \omega$.
We can express $M$ as a $2 \times 2$-matrix by defining the column vectors $|0\rangle = (1,0)$ and $|+\rangle = (1, 1)/ \sqrt{2}$,
$M = \dfrac{1}{4}
\begin{pmatrix}
3 & 1 \\
1 & 1
\end{pmatrix}, \qquad \mathrm{Tr}(M) = 1, \mathrm{Det}(M) = \dfrac{1}{8}$,
and solving for its eigenvalues:
$\mathrm{eig}(M) = \dfrac{1}{2} \left( \mathrm{Tr}(M) \pm \sqrt{\mathrm{Tr}(M)^2 - 4 \mathrm{Det}(M)}\right)
= \dfrac{1}{2} \left( 1 \pm \dfrac{1}{\sqrt{2}} \right) = \cos^2 \left(\frac{\pi}{8}\right)$.
The larger eigenvalues has the plus sign so
$\omega = \dfrac{1}{2} \left( 1 + \dfrac{1}{\sqrt{2}} \right) = \cos^2 \left(\frac{\pi}{8}\right)$.
$\dfrac{1}{4}
\begin{pmatrix}
3 - \omega & 1 \\
1 & 1 - \omega
\end{pmatrix}
\begin{pmatrix}
x \\
y
\end{pmatrix} =
\begin{pmatrix}
0\\
0
\end{pmatrix}$.
Working out the algebra, we obtain $y = (\sqrt{2}- 1)x$. Since we want the eigenvector to be normalized, we have
$x^2 + (\sqrt{2} - 1)^2 x^2 = 1 , \qquad \implies \qquad
x^2 = \dfrac{1}{4- 2\sqrt{2}} = \dfrac{4 + 2\sqrt{2}}{8} = \dfrac{1}{2} \left( 1 + \dfrac{1}{\sqrt{2}} \right) = \cos^2 \left(\frac{\pi}{8}\right) $.
Thus, the eigenstate with maximum eigenvalue $\omega = \cos^2 \left(\frac{\pi}{8}\right) $ is
$|m \rangle =
\begin{pmatrix}
x \\
y
\end{pmatrix} =
\begin{pmatrix}
\cos \left(\frac{\pi}{8}\right) \\
\sin \left(\frac{\pi}{8}\right)
\end{pmatrix}$
where $\omega$ is also Eve's optimal probability for guessing $x$.
So we have seen that for Eve who can prepare quantum states but has no quantum memory, her best strategy wins the guessing game with probability $\omega = \cos^2 \left(\frac{\pi}{8}\right) $ so the upper bound is $c = \cos^2 \left(\frac{\pi}{8}\right) $ for such an adversary.
That Eve is unable to always guess correctly means that there is some secret information that we may extract from $x$. Typically, this involves running the game independently many times until you can extract a sufficient number of secret bits.
 |
| If Eve plays the guessing game with a quantum memory then she can always win the game. Her winning strategy is to prepare an EPR pair, and send one qubit to Adam while keeping one to herself. Thus, whether Adam measures in the standard or Hadamard basis, Eve just needs to wait for Adam to announce his basis $\theta$ so she can measure her share of the EPR pair in the same basis and obtain the same bit value $x$. |
What happens if Eve is allowed to store some qubits? Then if you think about it for a bit, you will find that Eve can perfectly win the game. This is because all Eve needs to do is to prepare an EPR pair and keep one system for herself.
Because an EPR pair can be written as
$|\Phi\rangle = \dfrac{|00\rangle + |11\rangle }{\sqrt{2}}
= \dfrac{ |++\rangle + |--\rangle}{\sqrt{2}}$,
when Adam makes a measurement in either the standard or Hadamard basis, he gets a random outcome but he "steers" Eve's qubit to the same basis state as his qubit after the measurement. Eve just waits for Adam to reveal the basis $\theta$ and then she can measure her qubit in the same basis to get the same outcome as Adam.
Are we out of luck then, since we can not be sure if an adversary Eve has quantum memory or not? No, not yet since we know that entanglement is monogamous.
To restrict Eve's information about Adam's measurement results in the guessing game, we have to exploit both the uncertainty principle and the monogamy of entanglement. To make sure Eve does not gain any advantage from being able to store qubits, Adam needs to play with another honest party, Bob.
What happens is that both Adam and Bob receive qubits. Adam still picks the basis $\theta$ to measure his qubit to get an outcome $x$. Afterwards, Adam announces $\theta$ to both Bob and Eve. Bob will then measure his qubit in the same basis $\theta$ to get an outcome $y$. Eve will make some measurement on whatever quantum state she kept for herself to get a bit outcome $z$. The goal of the game is then for Eve and Bob to both correctly guess Adam's bit $x$, i.e., Eve and Bob win the game if $x = y = z$.
A full analysis of this monogamy-of-entanglement (ME) guessing game is a lot more involved so we will not go through it here. But what we can intuitively see is that if Bob tries to win the game all the time by being entangled to Adam with an EPR pair, then Eve will be completely disentangled with Adam and therefore the quantum state she stored will not have perfect information about $x$.
In fact, the analysis of the three-player ME guessing game shows that the optimal winning probability is the same as in the two-player uncertainty game with no quantum memory: in fact, Eve can play the ME game using her optimal strategy with classical resources only.
The analysis of the ME game has been used to show that BB84 is secure even for a receiving party who has untrusted measurement devices, and for one-round single-qubit position verification scheme.
References:
M. Tomamichel, S. Fehr, J. Kaniewski, S. Wehner, A Monogamy-of-Entanglement Game With Applications to Device-Independent Quantum Cryptography, New Journal of Physics 15 (2013) 103002.
No comments:
Post a Comment