In a generic search problem, we are given a set $S$ of $N$ items. Some of the items in the set are marked. Our task is to find a marked item in the set $S$.
You can think of a search problem like looking up a name in a list. In most cases, the list will be arranged in a way that makes finding names easier. For example, a list of names is often sorted alphabetically. Here we are talking about a list with no discernible ordering. In this case, the best we could do is to check each entry for the desired name.
In mathematical terms, a search problem involves a function $f$ which takes as input $x$ from the set $S$ of $N$ items, and outputs a bit, 0 or 1. The bit value tells us whether the input $x$ is a marked item or not. Thus, the goal in a search problem is to find a marked item in $S$, i.e an item $x$ such that $f(x)=1$. In this case, we say that $x$ is a solution to the search problem on $S$.
When we talk about the complexity of a search algorithm, then typically the only cost we count is the queries made to the function $f$. This is the number we will compare between classical and quantum methods.
Consider again the problem of searching a list of names. The function $f$ in this setting corresponds to a means of checking if an entry $x$ is the desired name. In practice, that might just mean reading the entry yourself, or maybe querying some machine that does this check for you. Whichever the case, the best you could do for an unstructured list is to query $f$ for each entry until you get to a solution, which might take around $N$ queries. Grover's algorithm solves the unstructured search problem using just around $\sqrt{N}$ queries, so the speedup we get is not as spectacular as in Shor's algorithm, but is no less significant.
Here I will describe Grover's algorithm. In order to be explicit with some of the calculations, I will be using a specific example: we are going to search for a unique solution in a set with $8$ items. This means we will consider a function $f$ that takes 3-bit strings as an input, i.e., the items in the set are labeled with bit strings, and outputs a bit $f(x)$, which tells us if $x$ is marked or not.
We will need some background material in order to discuss the details of the algorithm so we will go through them here briefly. First I will describe a few elementary quantum gates for building quantum circuits. In the figure below, the gates we consider are the NOT gate, the CNOT gate, and the Toffoli gate (these gates operate the same way on bits if we have classical Boolean circuits).
 |
| Some elementary quantum gates that we will use to construct larger quantum gates. |
The NOT gate is a single-qubit gate flips the computational basis states $|0\rangle$ into $|1\rangle$, and vice-versa. This is also known as the Pauli-$X$ gate.
The CNOT gate is a two-qubit gate that flips computational basis states in the second register (target qubit) if the first register has a bit value 1 (control qubit). It is known as an entangling gate for two qubits since if we prepare the control qubit in the state $|+\rangle = ( |0\rangle + |1\rangle )/\sqrt{2}$ and the target qubit in the state $|0\rangle$, then the output after applying a CNOT gate is
$ \text{CNOT} ( |0\rangle + |1\rangle )|0\rangle /\sqrt{2}
= \text{CNOT} ( |00 \rangle + |10 \rangle ) /\sqrt{2}
= ( |00\rangle + |11\rangle )/\sqrt{2}$,
which is an EPR pair.
The Toffoli gate, also known as the controlled-CNOT gate and was invented by Tommaso Toffoli, is a three-qubit gate that flips the computational basis states of the third qubit if and only if the first two qubits both have a bit value of 1. This gate is like a reversible version of the AND gate, which outputs 1 if and only if the two input bits are both 1. (A gate is reversible is we can determine what the input was if we are given only the output.)
In quantum theory, a quantum operation must be unitary if they are to preserve the total probabilities. This means that if we want to make a quantum gate $U_{f}$ that computes a function $f$, this gate must be reversible. Fortunately, in most cases, this just means that when we build $U_{f}$, we should have a register or wire that holds the input.
The figure below shows an oracle or black box for computing a function $f$ with a three-bit input and one-bit output. You will often see similar-looking oracles in texts about quantum algorithms. This is because for some computational problems, we are not so concerned with the details of how the function $f$ is computed, in which case, we think of how simple or complex an algorithm is only in terms of how many times we have to query the function $f$. For many problems, this already gives us a good idea if a problem is hard or easy to solve.
 |
| A standard quantum black box for the function $f$. It involves two sets of wires: a top set (here the top 3 wires) for the input to $f$ and a bottom set (here just the last wire since the output is 1 bit) for the output for $f$. |
Still you might be curious how a function $f$ might be implemented in practice. Later when we describe Grover's algorithm, we will consider an unstructured search problem on a set of 8 items with a unique marked item. In terms of the function $f$, this means we can label the items with 3 bits (000, 001, all the way to 111), and we are looking for which 3-bit string x gives $f(x) = 1$.
Let's suppose that $f(110) = 1$ so 110 is the unique solution to our search problem. Then one possible circuit that computes $f$ through a quantum gate $U_{f}$ is shown below. Observe that the circuit below uses two additional wires (the 4th and 5th wires from the top) that hold intermediate values of a computation. However, we use the trick of un-computation to reset these wires to their initial values (they start and end in state $|0\rangle$ ) so these wires can be discarded without affecting the qubits in the other wires. If you are thinking in terms of a black box $U_f$ then the 4th and 5th wires can be placed completely inside the black box.
 |
| While quantum algorithms are often described using quantum black boxes when the function $f$ is queried, in practice the black boxes have to be implemented using quantum gates. Here we present a quantum circuit for out example function $f$ which has a marked item $x = 110$. |
Another trick that will be useful to us is called the phase-kickback trick. Suppose we have a function $f$ with an input of $N$ bits and outputs a bit. We can construct a corresponding quantum gate $U_f$ that computes this $f$, which has a top wire of $N$ bits, and a bottom wire of 1 bit, as illustrated in the figure below. Let us examine what happens if we use an input of $|x\rangle$ on the top wire and $|-\rangle = ( |0\rangle - |1\rangle )/\sqrt{2}$ on the bottom wire:
$U_{f} |x\rangle |-\rangle = U_{f} (|x\rangle |0\rangle - |x \rangle |1\rangle )/\sqrt{2}
= (|x\rangle |f(x) \rangle - |x \rangle |\overline{f}(x) \rangle )/\sqrt{2} $
$ = |x\rangle ( |f(x) \rangle -|\overline{f}(x)\rangle )/\sqrt{2}
= |x\rangle (-1)^{f(x)} ( |0\rangle - |1\rangle )/\sqrt{2}
= (-1)^{f(x)} |x\rangle |-\rangle$
where $\overline{f}(x) = 1 \oplus f(x)$. So what we see is that the bottom wire receives a sign that depends on whether $f(x)$ is 0 or 1. However, since this phase depends only on what is on the top wire, we can think of this phase being "kicked back" onto the top wire (thus, the name phase kickback).
If you have read other references for Grover's algorithm, they will sometimes talk about an oracle or black box for the function $f$ that marks $x$ as a solution by multiplying it by -1. Now you know how such a black box can be built for $f$ using phase kickback.
 |
| The phase-kickback trick is often used to build a quantum gates that flips the phase of solution states given a quantum black box for computing $f$. Since the state $|-\rangle$ remains the same after, this wire can actually be considered as part of the black box for $f$. |
The last thing we we require is a quantum gate that flips the phase (maps $|x\rangle to -|x\rangle$) except when $x$ is the all-zeroes string. As we have already seen, this can be achieved using the phase-kickback trick on a quantum gate $U_{g}$ that computes the function $g$ where $g(000) = 0$ and $g(x) = 1$ otherwise. This is shown as a black box in the figure below. Note that because this operation flips a known state $|0\rangle$ and is independent of $f$, then we consider the operation to be cost-free (we don't count queries to $g$ when comparing the number of queries between classical and quantum algorithms).
 |
| A quantum gate for the function $g$ that flips the phase of all computational basis states except the all-zeroes string. Since this operation does not involve any queries to $f$, then we do not count the queries made to it. |
We do not need to know exactly how $g$ is computed in $U_{g}$ but for completeness I provided a sample quantum circuit for implementing $U_{g}$ below. Similar to what we had for $f$, the 4th and 5th wires from the top are additional wires for intermediate results, which would be fully contained within a black box for $U_g$.
 |
| A possible quantum circuit for implementing the black box $U_g$ in practice. |
Now we have all the ingredients to describe the steps in Grover's algorithm. Again, here we are solving specifically a search problem on a set of 8 items so we will use 4 qubits: 3 qubits are used for the input to $f$ and one qubit for the computed value of $f$.
In the preparation phase, we start with 3 qubits in state $|0 \rangle$ and one qubit in the state $|-\rangle$ in the last wire, which you have seen will be used for implementing phase kickback. Then we apply the Hadamard gate to each wire with a qubit in $|0 \rangle$. Recall that the Hadamard gate is the quantum gate that maps $|0\rangle$ to $|+\rangle$ and $|1\rangle$ to $|-\rangle$. The goal here is to prepare an equal superposition state for all possible inputs to $f$.
$ |0\rangle |0\rangle |0\rangle |-\rangle \mapsto |+\rangle |+\rangle |+\rangle |-\rangle $
Next is the iteration phase. Here we will apply an operation a certain number of times before measuring the qubits. We shall call the repeating operation the Grover operator $G$ and it involves the following steps: (i) apply $U_f$, (ii) apply Hadamard gates to all wires except the bottom wire with the $|- \rangle$, (iii) apply $U_g$, and (iii) apply Hadamard gates again to all wires except the bottom wire. The quantum circuit for $G$ is shown below.
 |
| The Grover operator $G$ that is repeated a number around $\sqrt{N}$ times during the iteration phase. |
In the iteration phase, we apply the Grover operator $m = \pi\sqrt{N}/4 $ times, rounded down to the nearest number. In our example $N = 8$ so $m = 2.221$, which is rounded down to 2.
We can also show how the quantum state in the wires change with each application of $G$. The calculation is straightforward but it can be rather tedious to illustrate step-by-step so we will only state the result after each application of $G$:
$ G G |+\rangle |+\rangle |+\rangle |-\rangle $
$= G (|0\rangle |0\rangle |0\rangle + |0\rangle |0\rangle |1\rangle +|0\rangle |1\rangle |0\rangle +|0\rangle |1\rangle |1\rangle
+|1\rangle |0\rangle |0\rangle + |1\rangle |0\rangle |1\rangle + 5 |1\rangle |1\rangle |0\rangle +|1\rangle |1\rangle |1\rangle ) |-\rangle /(4\sqrt{2}) $
$= (-|0\rangle |0\rangle |0\rangle - |0\rangle |0\rangle |1\rangle -|0\rangle |1\rangle |0\rangle -|0\rangle |1\rangle |1\rangle
-|1\rangle |0\rangle |0\rangle - |1\rangle |0\rangle |1\rangle + 11 |1\rangle |1\rangle |0\rangle -|1\rangle |1\rangle |1\rangle ) |-\rangle /(8\sqrt{2}) $
We end our quantum computation by measuring all the wires except the bottom one (with $|-\rangle$) in the computational basis to obtain some bit-string value, which we call $y$. From the calculation above, we see that we would get $y = 110$ with probability $(11/(8\sqrt{2}))^{2} = 0.945$ so with high probability, we will obtain the solution to our search problem. The quantum circuit for the Grover search in our example is illustrated in the figure below.
 |
| A quantum circuit for Grover's algorithm for our example function $f$ with marked item $y = 110$. Since $N = 8$ in our problem, $\pi \sqrt{N}/4 \approx 2.21$ which is 2 when rounded down, so the Grover operator $G$ is applied twice. |
To gain some intuition for why this quantum search algorithm works, it may be useful to understand what the operator $G$ does to the quantum state in the wires. Since an equal superposition state is prepared in the preparation phase, we can represent this quantum state in terms of a bar graph of the probability amplitude for each bit-string value. An equal superposition state means the bars in our graph will all be of the same height, illustrated as the blue bars in the diagram below.
 |
| What the Grover operator does on the probability amplitudes: Initially we have the same amplitude for each basis state, shown as the blue bars of same height. Next the gate $U_f$ flips the phase of the solution state, which can be seen in the orange bars. Finally, the rest of the Grover operator performs an inversion about the mean. Here the mean is indicated by dashed line. You can see this inversion about this line by comparing the orange bars to the gray bars. |
Now when we apply $U_f$, what happens is it flips the sign of the marked item. The rest of the operators in $G$ is actually a phase flip operator that flips the sign of the equal superposition state. Its net effect on the current quantum state is to flip the bar heights about the average bar height (which is the dashed line in the diagram). This is why the combination of $U_g$ sandwiched by Hadamard gates is sometimes called inversion about the mean.
Thus, in the iteration phase, we repeatedly apply a phase flip on the solution state and a mean inversion until the amplitude of the solution is large enough. In example, we saw that the amplitude for $y = 110$ increased by roughly $1/\sqrt{N}$ when $G$ was used so this is why we expect $\sqrt{N}$ application of $G$ gives the solution with high probability.
To summarize, Grover's algorithm for searching a set of $N$ items is run as follows:
(i) Start with $N$ qubits in $|0\rangle$ on the top register and a qubit in state $|-\rangle$ on the bottom register.
(ii) Apply Hadamard gates to the $N$ qubits on the top register.
(ii) Apply the Grover operator $G$ a total $\pi \sqrt{N}/4$ times, rounded down if needed.
(iv) Measure the $N$ qubits on the top register in the computational basis to obtain a bit string $y$.
(v) Verify that $f(y) =1$ so $y$ is a solution to the search problem.
We have seen how Grover's algorithm works and given some general idea of why it works but since the speed-up is not to large, is the result really that useful? While we often think of the algorithm in terms of searching a list, it is more accurate to think of it in terms of inverting a function. If we let $f(x) = z$ then the search problem is like trying to compute $x$ when you are given $z$. When thinking in these terms, then the possible applications become more apparent. Also, it turns out that you can show that for unstructured search, this is the best you can do, i.e., the number of queries used by Grover's algorithm is optimal.
One particularly useful application is in the collision problem in cryptography. In the simplest setting, we are asked in a given function $f$ is one-to-one (each possible input has a unique output) or two-to-one. Thus, solving the problem involves finding a pair of distinct values $x$ and $x'$ such that $f(x) = f(x')$. Knowing how to solve this problem is useful in cryptography because for many schemes employ functions whose security relies on the condition that collisions are hard to find. Grover's algorithm can be used in this instance to show that a scheme can be broken by a quantum computer.
And finally, even for unstructured search, a quadratic speedup may be significant in practice: it means a classical method that runs in 100 s might only take 10 s for a quantum computer.
References:
Ryan O'Donnell, Grover's Algorithm (2015).
Philip Kaye, Raymond Laflamme, and Michele Mosca, An Introduction to Quantum Computing (Oxford, 2007) chap. 8.
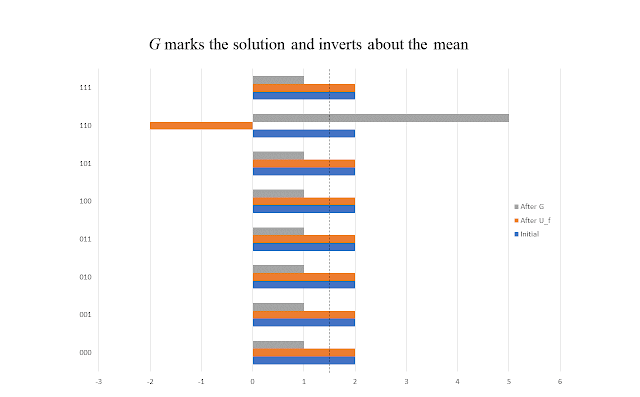
No comments:
Post a Comment