The quantum physics of smell

When I first heard about how quantum effects might be involved in the process of smelling, I was immediately fascinated by it. So much so that I searched for the original paper making such a proposal and studied what role quantum mechanics plays in the nose's ability to recognize odors. This entry is an attempt to explain what I've learned, in the simplest possible terms that I can make it.

To start, it is worth mentioning that much is already known about the smelling process. The 2004 Nobel Prize in Physiology or Medicine was awarded to Richard Axel and Linda Buck for their discoveries on odor receptors and how the signals from these receptors are amplified and processed. The basic idea is that odor molecules, or odorants, attach onto receptors that match their size and shape, in what is called a lock-and-key mechanism. Just as a lock can only be opened with a key of the right shape, an odor receptor is activated only if the right odor molecules comes along and 'plugs' it.

Despite the nice and simple picture it provides for how odors are recognized, the lock-and-key mechanism does have its limitations. One big problem is that it does not perfectly match with observations: some molecules of widely different structures carry similar odors (e.g., borane, thiols) while some molecules with just a few atoms changed or rearranged can have totally different smell characteristics (e.g., enantiomers).

In 1996, the biophysicist Luca Turin proposed that ultimately, the odor receptors respond not to the shape of molecules but to their molecular vibrations. He provided a detailed and plausible mechanism for how this happens via a quantum effect known as inelastic phonon-assisted electron tunneling. Before I get to that, I will try to explain quantum tunneling first.

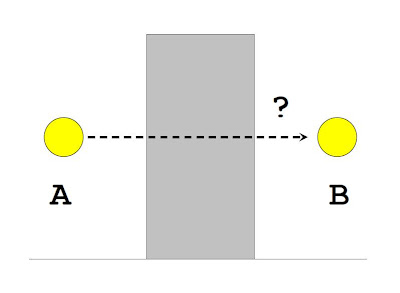
One can think of the tunneling process using the picture shown above. Imagine the yellow ball is at point A and it wishes to go to point B. However, there is a barrier that blocks its path. The question is, how can it get to the other side of the wall?

If the yellow ball is something like a tennis ball, that is, a classical object, then we know from experience that it can never go straight through the wall--it will just bounce off it. The only way to get it beyond the barrier is to provide it with enough energy so that it can jump over the wall and land on the other side.

Now if we imagine the yellow ball to be something like an electron, that is, a quantum object. Then something truly bizarre happens. Certainly, we can still make the electron scale the wall by giving it enough energy to jump the barrier. But even without any extra energy, there is a very small but non-vanishing chance that it will shoot past the barrier and appear on the other side, at point B. This is because quantum mechanics tells us that the probability of finding an electron in some location is given by a wave function ψ. As indicated in the picture, this wave function has a much smaller amplitudes at point B than at point A (if the ball starts at point A) but it is nonetheless not zero. This ability of quantum objects to penetrate barriers this way is what's called the quantum tunneling effect. This effect seems to play a key role in explaining how the smell of odorants are related to their molecular vibrations.

You may ask, why is the motion of quantum objects governed by this so-called wave function? Quite frankly, we don't exactly know why. We just know that our equations in quantum physics say this is so, and we know it works because it has been observed and verified in experiments many times. For example, the decay of radioactive material such as uranium is, in fact, a quantum tunneling process.

Finally, we show what it means to have inelastic quantum tunneling. In regular cases, when an electron shoots past the barrier and appears on the other side, it retains its energy. This is what's called elastic tunneling. Now it may be the case that the electron at point A loses some energy while crossing the barrier and ends up with a lower energy at point B. This is called inelastic tunneling. Because energy must be conserved, the lost energy must be emitted somewhere in the barrier and in many situations, it does so in the form of vibrations, which in particle form are called phonons. Such a process is called phonon-assisted tunneling, since it needs a phonon to take the 'garbage' energy out of the tunneling electron.

The crucial point here is that a phonon with precise energy is essential in completing the tunneling process: if the barrier doesn't permit vibrations with the required energy then the electron can't emit its excess energy and won't be able to tunnel through. This would be the case if region of point B is such that it can't hold electrons that are too energetic.

This is why this scenario has been referred to as the swipe card model--the electron can't access point B from point A without a valid swipe card, which in this case is a phonon with just the right amount of energy.  

(The equation in the diagram just says that the required energy V of the phonon is equal to the difference between the energy of the electron at points A and B--no more, no less.)  

If you're wondering what the heck a particle of vibration is, don't worry about it. Quantum physics is just weird that way--anything that can carry energy can be treated as a particle sometimes. In fact, that's related to the original meaning of the word 'quantum': a smallest discrete unit. Phonons just indicate that even vibrational energies come in indivisible chunks.

Now we are ready to explain how the tunneling effect might be involved in smelling. A diagram of an odor receptor binding site is shown above. The barrier in this case is actually the empty space within the binding site, the place where odor molecules of the correct shape and size fit into. This shows that the lock-and-key model stills plays a role in the process. Like in regular tunneling scenarios, we have two opposite sides for this barrier: a donor and an acceptor region of the receptor protein. The exact biological nature of the donor and acceptor is presently unknown.

A source of external electrons is needed (only free, excess electrons get teleported) and this is speculated to be some soluble electron donor in the cell fluid, perhaps a substance called NADPH (nicotinamide adenine dinucleotide phosphate). An excess electron is obtained from such a source and goes into the donor region, where it sits with energy E[D].

If the binding site has no odorant, the electron won't be able to tunnel through for the same reasons mentioned above: it has to be able to get rid of its excess energy by creating vibrations of the right frequency. The electron can do this if a suitable odorant is inserted in the binding site. (By suitable, we mean odorants with the right vibrational energy). If that is the case, the electron sweeps through the odor molecule, releases its excess energy V = E[D] - E[A] in the form of a phonon, and moves onto the acceptor with some lower energy E[A]. The presence of the electron in the acceptor then triggers the release of the G-protein, which initiates further signals that are eventually transmitted to the brain and registers a smell.

Again, just to reiterate: if the odorant has the wrong vibrational energies then the electron won't be able to produce a phonon with an energy that matches the energy difference between the donor and acceptor, in which case, the access to tunneling is denied.

For some extra technical detail, the G-protein (guanine nucleotide-binding protein, which plays a major role in transmitting chemical signals beyond cells) is connected to acceptor by a disulphide bridge (R-S-S-G). Because of the incoming electron, the disulphide bridge is chemically reduced (R-S-S-G goes to R-S-H + H-S-G),  freeing up the G-protein for further transduction activity.


References: 

L. Turin, "A Spectroscopic Mechanism for Primary Olfactory Reception", Chemical Senses 21 (1996) 773-91. 

M. I. Francoa, L. Turina, A. Mershin, and E. M. C. Skoulakisa, "Molecular vibration-sensing component in Drosophila melanogaster olfaction", PNAS 108 (2011) 3797–3802.

J. C. Brookes, F. Hartoutsiou, A. P. Horsfield, and A. M. Stoneham, "Could Humans Recognize Odor by Phonon Assisted Tunneling?", Physical Review Letters 98, (2007) 038101.

L. Turin, "The science of scent", TED Talks (2005).